Inertial Navigation Notes
Page Contents
References
- Strapdown Inertial Navigation Technology (IEE Radar, Sonar, Navigation and Avionics Series)
- Basic Inertial Navigation
- NED (North-East-Down) Frame
- How does an INS work?
- Towards understanding IMU: Frames of reference used to represent IMU orientation and how to visualize the circuit orientation using Vpython library
Pitch, Roll, Yaw, and Attitude
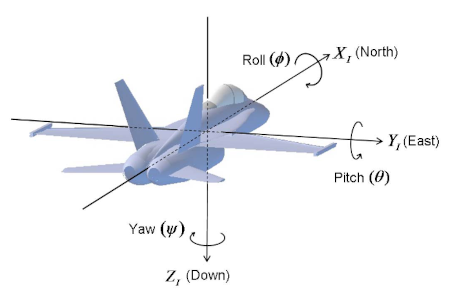
Image from https://atadiat.com/en/e-towards-understanding-imu-frames-vpython-visualize-orientation
Roll: Rotation about the forward body axis. It describes tilting left or right.
Pitch: Rotation about the lateral body axis. It describes tilting up or down.
Yaw: Rotation about the vertical body axis. It describes heading or turning left or right.
Attitude: The orientation of the sensor body relative to a chosen reference frame. It describes how the body axes are rotated with respect to a navigation frame such as North East Down or Earth centred Earth fixed. For exampl, an aircraft is flying straight east, wings level, with its nose raised slightly. Its attitude is:
- Roll = 0 degrees, no left or right tilt.
- Pitch = 5 degrees nose up.
- Yaw = 90 degrees, pointing east relative to north.
This single set of angles fully describes the aircraft orientation relative to the navigation frame.
Attitude can be represented by the vector [roll, pitch, yaw], but attitude itself is a three dimensional rotation, not inherently a vector. It is a rotation between coordinate frames.
Rotating Body Frame To Reference (Navigation) Frame
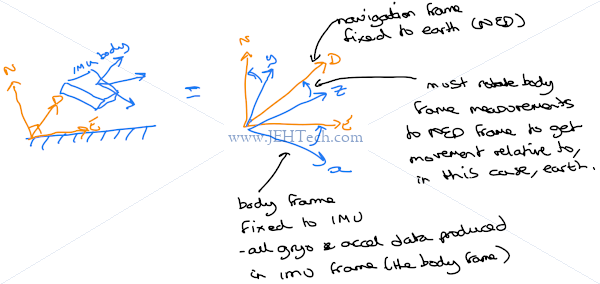
A 2D navigation example
A vehicle lets say, moving at a constant attitude.
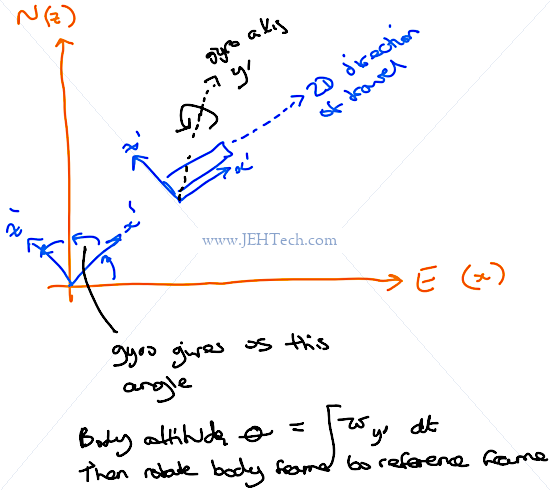
A gyro measures angular velocity,
Where
Once we have
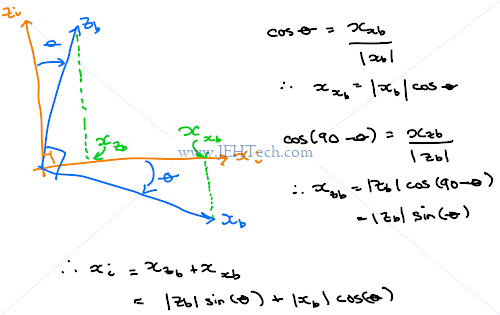
So we get:
And using similar reasoning:
These forces measured by the IMU are accelleration. Integrate to get velocity and again to get distance.